一、誤差的基本概念:
1.誤差的定義:
誤差=測得值-真值;
因此,誤差是一個值,數學上就是坐標軸上的一個點,是具有正負號的一個數值
2.誤差的表示方法:
① 絕對誤差:
絕對誤差=測量值-真值(約定真值)
在檢定工作中,常用高一等級準確度的標準作為真值而獲得絕對誤差。
如:用二等線紋玻璃尺校正全自動影像測量儀,二等線紋尺示值為300mm,校準全自動影像儀的示值為299.998mm,則全自動影像測量儀的測量誤差為-0.002mm。
② 相對誤差:
相對誤差=絕對誤差/真值X100%
相對誤差沒有單位,但有正負。
③ 引用誤差:
引用誤差=示值誤差/測量范圍上限(或指定值)X100%
引用誤差是一種簡化和實用方便的儀器儀表示值的相對誤差。
3.誤差的分類:
① 系統誤差:在重復性條件下,對同一被測量進行無限多次測量所得結果的平均值與被測量的真值之差。
② 隨機誤差:測量結果與在重復性條件下,對同一被測量進行無限多次測量所得結果的平均值之差。
③ 粗大誤差:超出在規定條件下預期的誤差。

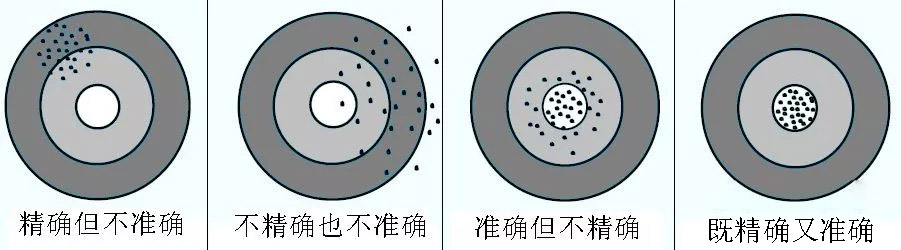
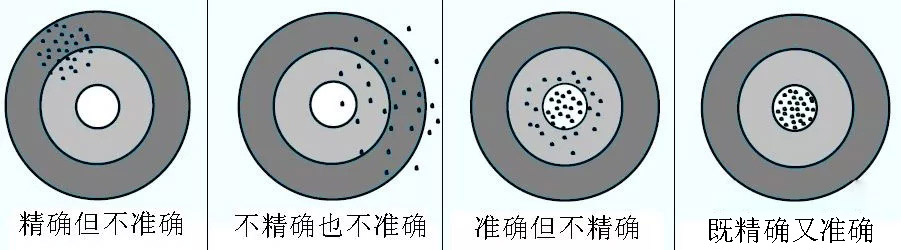
精度:
精度細分為:
準確度:系統誤差對測量結果的影響。
精密度:隨機誤差對測量結果的影響。
精確度:系統誤差和隨機誤差綜合后對測量結果的影響。
精度是誤差理論中的說法,與測量不確定度是不同的概念,在誤差理論中,精度定量的特征可用目前的測量不確定度(對測量結果而言)和極限誤差(對測量儀器儀表)來表示。對測量而言,精密度高的準確度不一定高,準確度高的精密度不一定高,但精確度高的準確度與精密度都高,精度是精確度的簡稱。目前,不提倡精度的說法。
一、三、測量不確定度
定義:表征合理地賦予被測量之值地分散性,與測量結果相聯系地參數。
① 此參數可以是諸如標準差或其倍數,或說明了置信水準的區間的半寬度。
② 測量不確定度由多個分量組成。其中一些分量可用測量列結果的統計分布估算,并用實驗標準差表征。另一些分量則可用基于經驗或其他信息的假定概率分布估算,也可用標準偏差表征。
③ 測量結果應理解為被測量之值的最佳估計,而所有的不確定度分量均貢獻給了分散性,包括那些由系統效應引起的(如,與修正值和參考測量標準有關的)分量。
由此可以看出,測量不確定度與誤差,精度在定義上是不同的。因此,其概念上的差異也造成評價方法上的不同。
四、測量誤差和測量不確定度的主要區別
1.定義上的區別:誤差表示數軸上的一個點,不確定度表示數軸上的一個區間;
2.評價方法上的區別:誤差按系統誤差與隨機誤差評價,不確定度按A類B類評價;
3.概念上的區別:系統誤差與隨機誤差是理想化的概念,不確定度只是使用估計值;
4.表示方法的區別:誤差不能以±的形式出現,不確定度只能以±的形式出現;
5.合成方法的區別:誤差以代數相加的方法合成,不確定度以方和根的方法合成;
6.測量結果的區別:誤差可以直接修正測量結果,不確定度不能修正測量結果;誤差按其定義,只和真值有關,不確定度和影響測量的因素有關;
7.得到方法的區別:誤差是通過測量得到的,不確定度是通過評定得到的;
8.操作方法的區別:系統誤差與隨機誤差難于操作,不確定評定易于操作;
誤差與測量不確定度是相互關聯的,就是說,測量誤差也包含不確定度,反之,評定得到的不確定度也還是有誤差。
|
序號 |
測量誤差 |
測量不確定度 |
|
1 |
有正負的量值,其測量結果減去被測量的真值 |
無符號的參數,用標準差或標準差的倍數或置信之間的半寬表示 |
|
2 |
表明測量結果真值 |
表明測量值的分散性 |
|
3 |
客觀存在不以人的認識程度而改變 |
與對測量,影響及測量過程的認識有關 |
|
4 |
由于真值未知,不能準確得到當用約定值代替真值,可得其估算值 |
可由依據實驗,資料,經驗等信息評定,從而可定量確定 |
|
5 |
按性質可分為隨機誤差和系統誤差 |
不確定度分量評定時一般不分其性質,若需要可表述為:由隨機效應引入的不確定度分量和由系統效應引入的不確定度分量 |
|
6 |
已知系統誤差的估值時,可以對測量結果進行修正,得到修正后的測量結果 |
不能用不確定度對測量結果進行修正。在已修正的測量結果的不確定度中應考慮修正引入的不確定度 |
精度是按照誤差的分類進行評價的,但在誤差合成的方法上與測量不確定度是不同的,系統誤差按照代數和合成,隨機誤差按方和根法合成,而系統誤差與隨機誤差的合成則有按標準差合成的,有按極限誤差合成的。因此,其合成的方法并不統一。



